Lekcja programowania: Algorytm Euklidesa - schemat blokowy

Podstawa programowa z informatyki podkreśla znaczenie algorytmicznego myślenia. Algorytm Euklidesa poszukiwania największego wspólnego dzielnika dwóch liczb naturalnych (NWD), jako jedyny jest wymieniony z nazwy w podstawie programowej klas VII i VIII.  Jest zatem szczególnie ważny. Jego realizacja w obu wersjach iteracyjnych, metodą przez odejmowanie i metodą przez dzielenie, jest obowiązkowa. Z zapisów podstawy programowej wynika, że uczeń powinien stosować  różne sposoby przedstawiania algorytmów w tym w postaci schematów blokowych dlatego przedstawię w niniejszym materiale możliwie kompletny sposób realizacji tego tego tematu w schemacie blokowym. 

Do wykonania schematu wybrałem program Magiczne Bloczki w wersji 1.0.2.22, która ma licencję Freeware .  Program umożliwia wstawianie bloczków na planszę i łączenie ich strzałkami w schemat blokowy. Wbudowany prosty język sprawia, że możliwe jest sprawdzanie działania  schematu.  Świetnie sprawdza się możliwość uruchomienia układu wraz z oknem, w którym dynamicznie podczas wykonywania algorytmu w sposób ciągły lub krok po kroku, widoczne są kolejne wartości zmiennych. Więcej o programie można znaleźć na stronie producenta erisoftware.pl

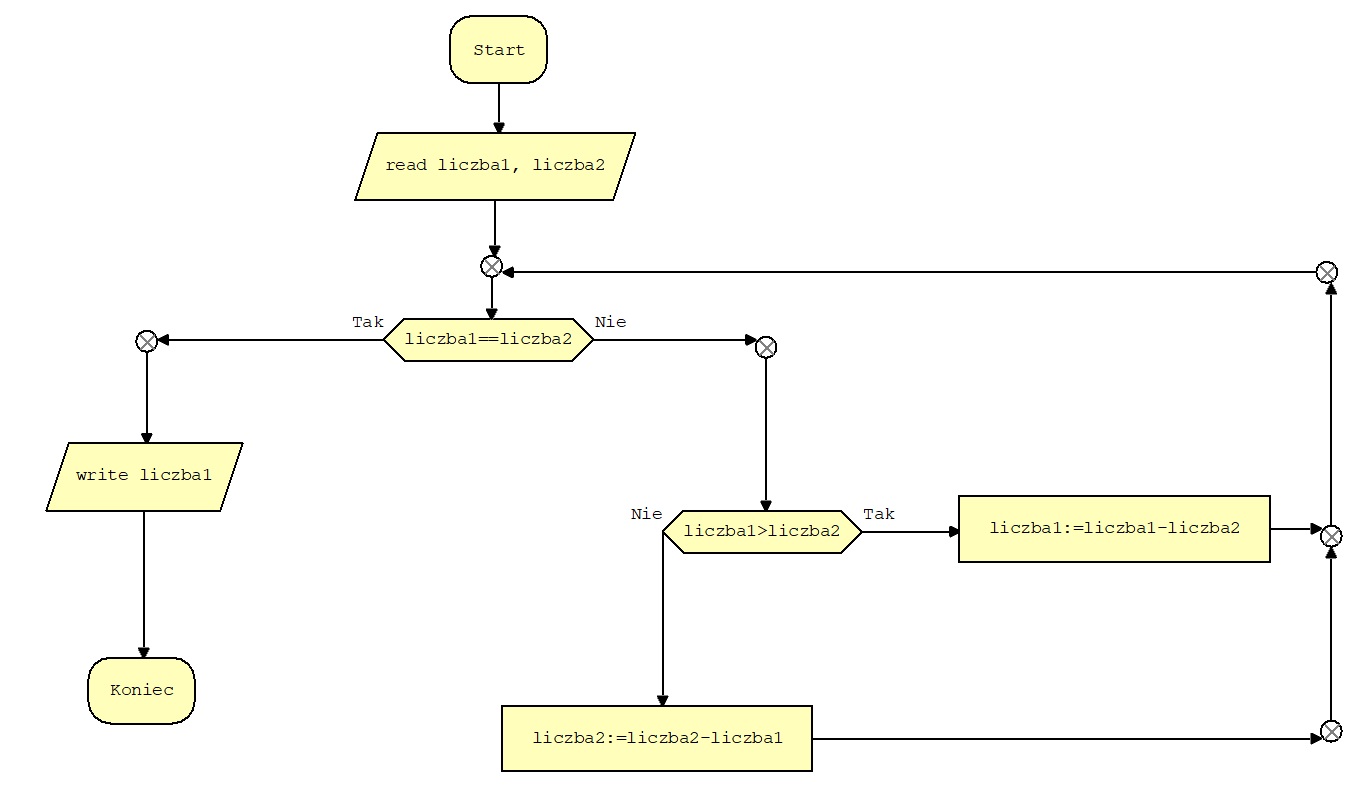
Powyższy schemat przedstawia algorytm Euklidesa obliczający NWD – metodą przez odejmowanie.

Po obowiązkowym bloku „Start” następuje wczytanie zmiennych liczba1 i liczba2 (read liczba1,liczba2). Następnie rozpoczyna się pętla, która będzie działała dopóki liczba1 i liczba2 nie są sobie równe. W pętli sprawdzane jest, która z dwóch liczb jest większa po to by w kolejnym kroku do większej podstawić różnicę większej  i mniejszej liczby. Na przykład jeżeli liczba1>liczba2 to podstawiamy  do liczba1 różnicę liczba1-liczba2 (liczba1:=liczba1-liczba2, := znak podstawiania). Podczas kolejnych przebiegów pętli , w skutek odejmowania i podstawiania różnicy liczb do większej z nich, liczby zrównają się. Po spełnieniu warunku ( liczba1==liczba2, == znak równości),  nastąpi wyjście z pętli. Teraz możemy wyprowadzić jedną ze zmiennych liczba1,liczba2  jako największy wspólny dzielnik (write liczba1). Blok „Koniec” jest obowiązkowym elementem schematu.

Warto zwrócić uwagę uczniom, że wadą tego algorytmu jest potencjalnie duża ilość operacji jeżeli różnica pomiędzy liczbami jest znacząca.

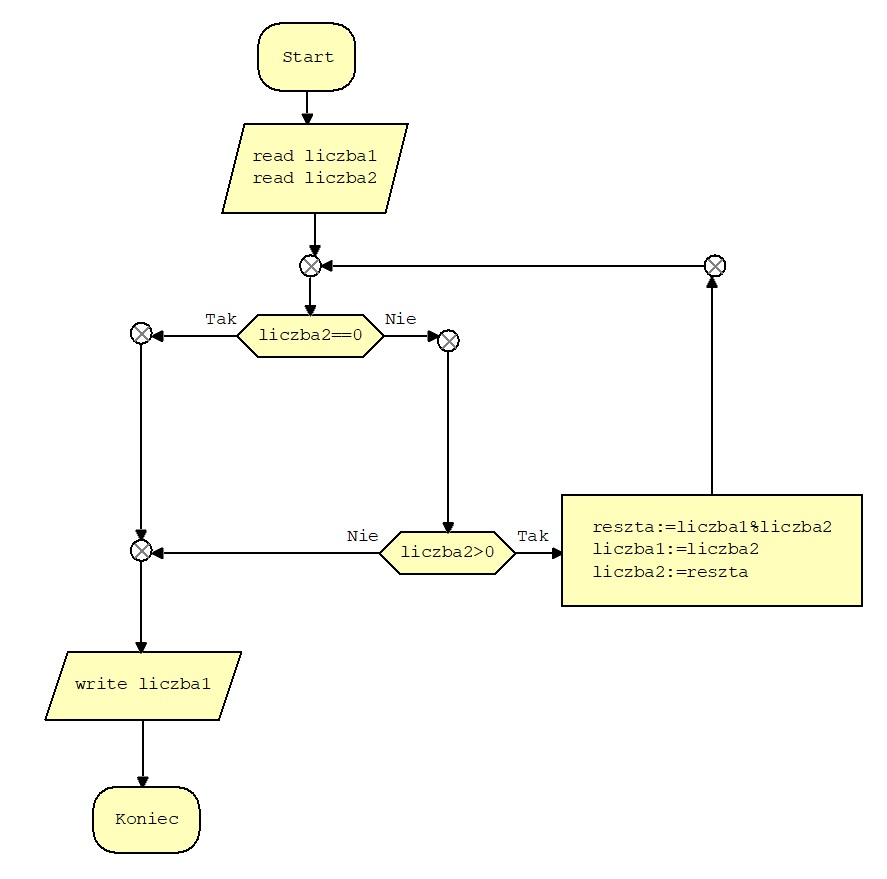
Drugą wersję algorytmu Euklidesa – metodą przez dzielenie, przedstawiam na schemacie powyżej.

Po bloku „Start” następuje wczytanie obu liczb (read liczba1, read liczba2). Następuje sprawdzenie czy liczba2 ma wartość 0 (liczba2==0). Właściwa pętla poszukująca NWD – metodą przez dzielenie będzie działała dopóki liczba2 jest większa od 0 (liczba2>0). Obliczana jest reszta z dzielenia liczba1 przez liczba 2 i podstawiana do zmiennej reszta (reszta:=liczba1%liczba2,  % - operator modulo ). Następnie podstawiamy do liczba1 wartość liczba2 (liczba1:=liczba2) a do zmiennej liczba2 wartość  reszta (liczba2:=reszta) . Wyjście z pętli nastąpi gdy liczba2 osiągnie wartość 0. Wtedy wyprowadzamy liczba1 jako NWD.

Metoda przez dzielenie jest bardziej wydajna, lepiej sprawdzi się w przypadku liczb między którymi jest duża różnica.  

Przejrzystość schematu blokowego i możliwość jego uruchomienia w środowisku Magiczne Bloczki, świetnie sprawdzą się na etapie tłumaczenia działania algorytmu. 

W kolejnym materiale przedstawiam implementację obu wersji algorytmu Euklidesa w  Scratch i Pythonie.

Zapraszam na  warsztaty z cyklu jak uczyć programowania organizowana w naszym ośrodku doskonalenia.

 

Marek Wróblewski

marek.wroblewski@odn.slupsk.pl